【純正律】
純正律とは、ある主音(=楽曲の中心となる音)を中心として、その主音と他の音が最も調和するように音の高さを決定する方法のこと。
調が一定であるとき、複数の音の調和度が極めて高くなるという利点がある一方で、転調すると調和度が大きく低下するという欠点がある。
【平均律】
平均律とは、いかなる調の楽曲であっても音同士の調和度を一定に保つために、西洋音楽の1オクターブ内の12種類の音が等間隔に並ぶように音の高さを決定する方法のこと。
調が変化しても、複数の音の調和度が高く安定した響きを得られるという利点がある一方で、純正律のような完全に調和した音は再現できないという欠点がある。
音の高さの相互関係のことを「音律」と呼びます。この音律を決定するための方法には、大きく分けて「純正律」と「平均律」の2種類の考え方があります。
このページでは、複数の音の響きを左右する音律や音の高さの種類について確認した後に、純正律と平均律とは具体的にどのようなものであるのか、違いについて見ていきます。
音律とは?音の種類と並び方
音楽では、高さの違う音を組み合わせてメロディや和音をつくり出します。
そのため、音の高さをどのように定めるかということは、音楽の根幹に関わるほど重要な問題なのです。
音の高さは、音の振動数(=周波数)によって決まります。私たちが耳にする音の正体は、振動する波が空気などを伝わったものなのです。
私たちは、振動数が大きくなるほど音を高く感じ、振動数が小さくなるほど音を低く感じます。
そして、音の高さ(=振動数)の異なる複数の音を組み合わせることで、音楽が形づくられているのです。
この時、音楽で使用する複数の音の高さの並び方を音楽的・数学的に決定するための考え方のことを「音律」と呼びます。
音律の歴史は、ピタゴラスによって「ピタゴラス音律」が考案された紀元前にまでさかのぼります。
それから、先人たちによって数多の試行錯誤がなされ、様々な音律が生み出されてきました。
数多くある音律の中で、現代でも重要な位置を占めている音律が2つあります。その2つの音律とは、「純正律」と「平均律」と呼ばれるものです。
1オクターブには12種類の高さの音がある
純正律と平均律に話を移す前に、音楽における「音の高さ」について理解を深めておきましょう。
西洋音楽では、「①ド・②ド♯(レ♭)・③レ・④レ♯(ミ♭)・⑤ミ・⑥ファ・⑦ファ♯(ソ♭)・⑧ソ・⑨ソ♯(ラ♭)・⑩ラ・⑪ラ♯(シ♭)・⑫シ」の12の高さの音が使用されます。
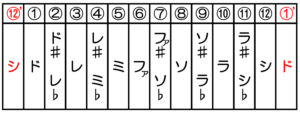
そして、不思議なことに、ある音が別の音の2の倍数(1/2・2・4・8など)の振動数であるとき、私たちはそれらの2つの音を同じ種類の音だと感じます。
たとえば、現代の西洋音楽においては、「ラ」の音の振動数を440Hz(ヘルツ・振動数の単位)と定めています。そして、1/2倍である220Hzの音や2倍である880Hzの音を、私たちは同じ「ラ」の音であると感じます。
そのため、ある音とオクターブ違いの同じ音との関係が2の倍数であることは、どの音律においても共通です。
しかしながら、低いドと高いド、低いラと高いラなどの同じ音同士と違い、ドとレ や レとミなどの違う種類の音同士の距離は、一定であるとは限りません。
実は、西洋音楽に用いられる12種類の音は、目的に応じて様々な音の高さの並べ方が模索されてきたのです。
調の変化と音の高さの関係
なぜ、西洋音楽における12種類の音の高さの相互関係は必ずしも一定ではないのでしょうか。
音の高さの相互関係が変化し得る理由は、「調」にあります。
実は、西洋音楽の12種類の音は、全てが同じようにうまく調和するわけではありません。
たとえば、一般的に「ド」の音は「ファ」や「ソ」の音とよく協和する一方で、「レ」や「シ」などの音との協和度は高くありません。
したがって、音楽をつくる際には、主役となる音(=主音)を決め、主音とよく調和する音を中心に楽曲が構成されます。
この時の、楽曲における主音と、主音と調和する音をピックアップしたもの(=音階)が作り出す曲の雰囲気を、「調」と呼びます。
つまり、音楽には楽曲の主役となる主音があり、12種類の音の中のうち主音と調和するいくつかの音が、楽曲の中で重要な役割を果たすのです。
すなわち、主音が異なれば、よく使われる音も異なってくる、ということを意味します。
ここで問題となるのが、「転調」です。
入門曲のような短い曲では、始めから終わりまで1つの調だけで完結することもあります。
しかしながら、曲がむずかしくなるにつれて、ある調から別の調へと移動する「転調」が行われるようになります。
「転調」が行われるということは、楽曲の主音が変化するということです。そして、主音が変化するということは、よく使用される音(=音階)の種類も変化することを意味します。
すなわち、「転調」の頻度が多いほどよく使用される音が変化するのに対して、「転調」が0に近いほど、よく使用される音も固定的になるのです。
音律が一定ではない理由は、この転調による音階の変化があるからです。
純正律とは?1つの調のみで最も調和する音律
転調がなければ、主音をある1つの音に固定し、他の音の高さを主音とよく調和するように調節することで、調和度の高い響きを得ることができます。
このように、ある主音(=楽曲の中心となる音)を中心として、その主音と他の音が最も調和するように音の高さを決定する方法のことを、純正律と呼びます。
基本的に、複数の音が共鳴しているとき、音の高さの整数比が小さいほど協和度が高くなります。
たとえば、ある音と別の音の振動数の整数比が81/64、256/243のように大きい数で表されるものより、5/4、3/2のように小さい数で表される関係の方が、よく調和するということです。
歴史の古いピタゴラスの音律では、「ド」に対する「ミ」の周波数比は81/64で、調和度は高くありませんでした。
これが純正律になると、「ド」に対する「ミ」の周波数比は、5/4に調整されます。
同様にして、ある主音に対する純正律は、以下の振動数で表されます。
※今回はわかりやすいように「ド」を主音としています。
ド 1 レ 9/8 ミ 5/4 ファ 4/3 ソ 3/2 ラ 5/3 シ 15/8 【表】小方厚「音律と音階の科学」(講談社)より抜粋。
このように、純正律では、主音と各音との振動数の比が比較的単純であり、よく調和するように調整されているのです。
数値では紹介していませんが、純正律では主音と各音の整数比だけでなく、となり合う音同士の振動数の比も単純になるよう調整されています。
ところが、このように調和度の高い単純な振動数の整数比は、主音が一定である場合にのみ実現します。
これが、転調して主音が変わってしまうと、振動数の整数比が大きくなってしまいます。
たとえば、「レ」を主音とした場合の「ラ」との音の高さの整数比は、40/27となります。また、「ファ」を主音とした場合のは「シ」との音の高さの整数比は45/32です。
このように、純正律の欠点は、転調によって調和度の低い音の組み合わせが生まれてしまうことにあります。
このような欠点を補うために、転調にも対応できる魔法のような音律が考案されました。それが、「平均律」なのです。
平均律とは?どの調でもほど良く調和する音律
西洋音楽では、多くの楽曲で「転調」が行われます。
転調があるため、主音や調が変化しても音の調和度が下がってしまわないような音律が求められていました。
そのために、12の音の高さを等間隔に並べた音律が考案されました。
このように、いかなる調の楽曲であっても音同士の協和度を一定に保つために、西洋音楽の12の楽音の音の高さを等間隔に並べたものを、「平均律」と呼びます。
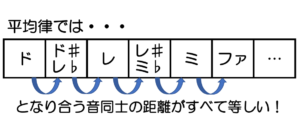
平均律では、となり合う音同士の距離(=音程)をすべて一定に保つことで、純正律の弱点を補い、調和度を落とさずに転調することを可能にしています。
ところで、となり合う音の音の高さを等間隔に並べると述べましたが、これは正確ではありません。
正確には、となり合う音同士の差(たし算)が同じなのではなく、となり合う音同士の比(かけ算)がすべて等しいのです。
具体的には、ある音の振動数に1.0594という数字をかけると、1つ高い音の振動数とほぼ同じ音の高さになります。
たとえば、「ド」の振動数に1.0594をかけると、「ド♯(レ♭)」の振動数とほぼ一致します。同様に、「ド♯(レ♭)」の振動数に1.0594をかけると、「レ」の振動数とほぼ一致します。
このように、不思議ではありますが、音と音の間隔が同じ差(たし算)ではなく同じ比(かけ算)であるときに、私たちは音が等間隔に並んでいると感じるのです。
ところで、ある音の高さに1.0594という数字をかけると1つ高い音の高さとほぼ同じになると述べましたが、これには理由があります。
実は、1オクターブを12の音で割り切ろうと思っても、割り切ることができません。
そのため、ある音ととなりの音との比は、1.0594・・・と無限に続く無理数(割り切れない数字)になってしまうのです。
このように、1オクターブを12の音で割り切ることができないために、音と音を組み合わせたときに、わずかなズレが生じてしまいます。
となり合う音同士の距離を等間隔にしようとすることでわずかなズレが生じるため、平均律は、純正律ほど高い音と音との調和を生み出すことができません。
これこそが、平均律の弱点なのです。平均律の欠点は、複数の音を組み合わせたときにほんのわずかなズレがあるために、純正律のように完全に調和した音の響きを得ることができないのです。
純正律と平均律の違いをまとめると?
ここまでで純正律と平均律それぞれの考え方について確認してきました。
では、純正律と平均律の意味を踏まえた上で、2つの違いを整理しておきましょう。
- 純正律はある特定の調でのみ最大限の調和が得られるのに対して、平均律はどの調でも(純正律には劣るが)安定した調和が得られる。
- 純正律は主音との距離で音の高さが決められるためとなり合う音同士の感覚は一定ではないが、平均律ではとなり合う音同士の感覚は常に等間隔である。
- 純正律は転調のない楽曲で平均律より調和した響きを得られるが、平均律は転調のある楽曲でどの調でも安定した調和のある響きが得られる。
純正律と平均律の2つの違いを整理してみると、純正律と平均律には、それぞれ他方にはない良さがあることがわかります!
平均律の利点は欠点を補って余りある
ここまで確認してきたように、平均律と純正律には、それぞれのメリットとデメリットがあります。
【 メリット 】調が一定であるとき、複数の音の調和度が極めて高くなる
【デメリット】転調すると調和度が大きく低下する
【 メリット 】調が変化しても、複数の音の調和度が高く安定した響きを得られる
【デメリット】純正律のような完全に調和した音は再現できない
複数の音の振動数に少しのズレがあるとはいえ、平均律のズレはほんのわずかです。
そして、レベルの高い楽曲では転調が頻繁に行われるため、一般的なピアノに用いられる音律はどうしても平均律に軍配が上がってしまうのです。
私たちが普段用いるピアノのほとんどが平均律によって調律されています。
今日では、転調などが頻繁に行われるような長大な作品であっても、作品全体を通して安定感のある響きで演奏されます。
このような安定した調和のある響きは、先人たちが試行錯誤の上に生み出した「平均律」のもとで成り立っていたのでした!
↑チャンネル登録お願いします↑
【ソナチネ第5番 / ベートーヴェン】↑チャンネル登録お願いします↑
【ピアノ歴1年半の初心者がトルコ行進曲に挑戦】↑チャンネル登録お願いします↑







